On the mechanisms

Authors: Edward van Dijk, Viktor Haaksman

Parts of this chapter have been published in Water Research 216, 118365 (2022) [van Dijk et al., 2022].

Abstract

In this chapter a mathematical framework was developed to describe aerobic granulation based on 6 main mechanisms: microbial selection, selective wasting, maximizing transport of substrate into the biofilm, selective feeding, substrate type and breakage. A numerical model was developed using four main components; a 1D convection/dispersion model to describe the flow dynamics in a reactor, a reaction/diffusion model describing the essential conversions for granule growth, a setting model to track granules during settling and feeding, and a population model containing up to 100,000 clusters of granules to model the stochastic behaviour of the granulation process. With this approach the model can explain the dynamics of the granulation process observed in practice. This includes the presence of a lag phase and a granulation phase. Selective feeding was identified as an important mechanism that was not yet reported in literature. When aerobic granules are grown from activated sludge flocs, a lag phase occurs, in which few granules are formed, followed by a granulation phase in which granules rapidly appear. The ratio of granule forming to non-granule forming substrate together with the feast/famine ratio determine if the transition from the lag phase to the granulation phase is successful. The efficiency of selective wasting and selective feeding both determine the rate of this transition. Breakup of large granules into smaller well settling particles was shown to be an important source of new granules. The granulation process was found to be the combined result of all 6 mechanisms and if conditions for one are not optimal, other mechanisms can, to some extent, compensate. This model provides a theoretical framework to analyse the different relevant mechanisms for aerobic granular sludge formation and can form the basis for a comprehensive model that includes detailed nutrient removal aspects.

Introduction

Fig. 41 Graphical abstract.

The process of aerobic granulation is influenced by many factors [Winkler et al., 2018]. Factors often described are hydrodynamic shear [Liu and Tay, 2002, Tay et al., 2001, Wu et al., 2020], physical selection on settling velocity [McSwain et al., 2004, van Dijk et al., 2020], the flow regime during contact of the sludge with influent [Haaksman et al., 2022, Lochmatter et al., 2014, Rocktäschel et al., 2013], dissolved oxygen concentration [Mosquera-Corral et al., 2005], feast/famine ratio [Beun et al., 2002, Cofré et al., 2018, de Kreuk and van Loosdrecht, 2004], influent substrate composition [Layer et al., 2019, Pronk et al., 2015], organic loading rate [Iorhemen and Liu, 2021], quorum sensing [Wang et al., 2017] and aggregation through EPS [Liu et al., 2010]. It is unclear which factors matter most and how their interplay is affected by the process conditions applied. A framework for biofilm morphology has been proposed [Picioreanu et al., 1998], but this framework only explains granule stability on the micro-scale, but it cannot explain granulation dynamics on a reactor scale. For anaerobic granular sludge, such a framework has been developed [Beeftink and van den Heuvel, 1990], but this framework is not as such applicable for aerobic granular sludge.

Fig. 42 Typical startup of an aerobic granular sludge reactor from flocs, showing an initial lag phase with slow improvement of the sludge morphology, followed by the granulation phase, where granules appear in the reactor. The colours indicate the size of the biomass aggregates, showing proto-granules and flocs (< 200 µm), small granules (>200 µm) and large granules (>200 µm). Data derived from the Nereda^® reactor in Utrecht, the Netherlands.

When a AGS reactor is seeded with activated sludge, under the right circumstances, granular sludge will develop from flocculent sludge. In practice this granulation process shows dynamics that are not easily explained. The granulation process commonly has a lag phase, in which not much change in the granulation grade (biomass fraction of the granules) seems to happen. Secondly, there is the granulation phase, in which granules start to appear in the reactor and the granulation grade increases (Fig. 42). The reason behind the lag phase and the trigger for the sudden start of granulation is unclear. We hypothesize that there are six main mechanisms that are of most importance for successful granulation (Fig. 43).

Microbial selection is important for the formation of granules. It has been shown that a stable dense biofilm can be best achieved, when the uptake rate of substrates is lower than the transport rate of the substrates into the granules [van Loosdrecht et al., 2002] . Therefore, the process is optimized towards organisms that anaerobically sequester readily biodegradable substrate by converting it into storage polymers and subsequently utilizing these polymers for aerobic growth [de Kreuk and van Loosdrecht, 2004, Nicholls and Osborn, 1979, Smolders et al., 1994] . This effectively separates the substrate uptake and the growth into two processes (called feast and famine). Phosphate accumulating organisms (PAO) and glycogen accumulating organisms (GAO) are examples of species that can make this split and these organisms are commonly observed in full-scale aerobic granular sludge processes [Ali et al., 2019] . Not all substrates can be sequestered anaerobically into storage polymers for aerobic growth of bacteria in the granules. We call these substrates, NGFS. Substrates that can lead to growth of aerobic granules (e.g. volatile fatty acids, but also readily biodegradable substrates that can be converted anaerobically) we call GFS.

Physical selection is also an important driver for growing aerobic granular sludge [Beun et al., 2002, de Kreuk and van Loosdrecht, 2004, Morgenroth et al., 1997, Qin et al., 2004] . AGS has advantageous settling properties compared to activated sludge flocs [Heijnen and van Loosdrecht, 1998, Morgenroth et al., 1997] . In AGS reactors flocs will always be present to some extent [Pronk et al., 2015] as not all carbon sources present in sewage can be converted to storage polymers during anaerobic feeding [Layer et al., 2020] . Therefore, it is needed to preferentially remove the flocculent sludge fraction with the excess sludge to give granules a competitive advantage. This is achieved by using the differential settling velocity between flocculent and granular sludge [Liu et al., 2005, van Dijk et al., 2020] . This is called the physical selection pressure.

Another well-known driver is maximizing transport of substrate into the biofilm. Higher substrate concentrations in the bulk liquid result in a deeper penetration of the substrate in the biofilm [Arvin and Harremoes, 1990] . This helps to grow and support a thicker biofilm. In AGS reactors a higher substrate concentration is achieved by either pulse feeding at the start [Beun et al., 2002] or more practical relevant by plug flow feeding from the bottom of the reactor [de Kreuk and van Loosdrecht, 2004, Pronk et al., 2015] . This gives a competitive advantage for larger granules. Larger granules settle faster than smaller granules and flocs, and therefore accumulate at the bottom of the settled sludge bed [van Dijk et al., 2020] . Feeding from the bottom therefore results in a longer contact time with the influent and contact with higher substrate concentrations for the larger granules. As a result, they will have more opportunity for growth than smaller fraction. Hence the term selective feeding.

Aerobic granules go through a typical life cycle that has a strong influence on the granulation process and reactor performance. When an AGS reactor is seeded with activated sludge flocs, these flocs will first form proto-granules. Flocs and proto-granules share similar bulk settling properties. An important difference is that the proto-granules already have the granular morphology but are smaller than 200 µm, which is considered to be the minimum size for an aggregate to be called an aerobic granule [de Kreuk et al., 2007] . Proto-granules already have been observed in conventional activated sludge processes, especially in systems with high anaerobic food to mass ratios, unmixed in-line fermentation, and a high influent soluble COD fraction [Wei et al., 2020] . Proto-granules are embedded in the floc matrix and settle together with the flocculent material.

Biological conversions in proto-granules are comparable to conversions in flocs, because the small radius of the proto-granules allows for full penetration with oxygen. Simultaneous nitrification and denitrification (SND) thus will be limited to very low DO conditions. When proto-granules grow out into small granules (> 200 µm), these small granules will settle significant faster and independent of the flocculent mass. The result is that small granules can experience the benefits regarding sludge selection, remain longer in the reactor with selective wasting and receive more influent with bottom feeding. When the granules continue to grow, the biofilm kinetics become more pronounced and full penetration of oxygen is less likely and SND will increase. Large granules (> 200 µm) are more susceptible to breakage [de Graaff et al., 2020] . When a granule breaks into smaller pieces some will be spilled and others will become a seed for new granules, restarting the granule life cycle. Thus we hypothesized that breakage of granules is an integral part of the granulation process, similar as proposed for anaerobic sludge [Beeftink and van den Heuvel, 1990] .

The aforementioned factors for aerobic granulation are not absolute. For example, only part of the substrate of domestic wastewater can be taken up anaerobically by the AGS directly or after fermentation. Still, it is possible to grow AGS on the complex composition of domestic wastewater [Layer et al., 2019, Pronk et al., 2015] . The selection pressure applied in full-scale reactors will be less effective than in lab-reactors, because of less favourable H/D ratios and other scaling factors. Apparently, the favourable mechanisms can be allowed to be non-optimally implemented to a certain extent without harming the granulation process. It is however unclear, how the different mechanisms influence one another positively or negatively if the process conditions become less favourable.

Analysis of the quantitative interplay between the aforementioned mechanisms in combination with varying process conditions requires a mathematical modelling approach. A mature granular bed in practice exists of a collection of granules with sizes up to 5 mm [van Dijk et al., 2020] . For the purpose of this study, a framework was required in which the lifecycle of granules could be tracked. Simulated granules should be allowed to have different time-variable spatial positions in the reactor and should be exposed to different bulk-liquid conditions, within a cycle and from one cycle to the next. This approach is required to capture the stochastic properties of an AGS system. Several models are available describing the AGS process with different emphases [Baeten et al., 2019] . Models that describe granulation as the development of a characteristic mean granule size [Ni and Yu, 2010, Yang et al., 2004] or assume a single granule size to study, for example, microbial speciation in granules and nutrient removal [Xavier et al., 2007, de Kreuk et al., 2007] are not suitable for the purpose of this study. The same holds for models that assume successful granulation using a fixed granule size distribution to investigate reactor performance [Dold et al., 2019, Layer et al., 2020] . Models with a dynamic granule size distribution [Beeftink and van den Heuvel, 1990, Li and Li, 2009] often use a PBM to describe the number of granules in a certain size class and the processes that influence these amounts (i.e. growth and detachment) via transitions from or to another size class. However, the available PBMs are only suited for completely mixed reactors, not for typical AGS reactors with combined spatial and temporal differences between the conditions experienced by aggregates. We hypothesized that the process for aerobic granulation can be described by six mechanisms (Fig. 43) with a minimal required description of the biological conversions, tracking the development of individual granule clusters in the reactor over time.

Fig. 43 A graphical representation of the six mechanisms for granulation: (1) microbial selection, (2) selective wasting, (3) maximizing transport of substrate into the biofilm, (4) selective feeding, (5) (non-) granule forming substrate, (6) breakage of granules.

In this study, we aimed to understand the underlying principles for aerobic granulation. A mathematical model was constructed that describes the full life cycle of aerobic granules. We performed a sensitivity analysis on the six mechanisms proposed and we evaluated their individual contribution to the granulation process.

Methodology

A model was developed integrating several sub-models describing all the proposed mechanisms responsible for the granulation process. The main process steps in current full-scale AGS reactors according to the Nereda^® concept are the feeding phase, in which fresh influent is fed to the reactor from the bottom, the reaction phase, where the wastewater is cleaned by different aeration strategies and finally the settling and decanting phase, in which the selective wasting takes place. In full-scale applications feeding and effluent decanting happens simultaneously [Giesen et al., 2013, Pronk et al., 2015].

Theoretical background

Biomass morphology

The morphology of biofilms is dependent on a combination of convection, diffusion, reaction, growth and detachment [Picioreanu et al., 2000]. All biomass clusters are assumed to have constant smooth and spherical morphology with a constant density. This specific biofilm morphology occurs when substrate uptake is limited by the maximum biomass specific uptake rate and not by transport [Picioreanu et al., 2000]. Since substrate uptake (anaerobic) is uncoupled from growth (aerobic) in full-scale AGS, a smooth, spherical biofilm morphology was assumed for all simulations. Wherever the distinction is made between flocs and granules, this is solely based on the sludge particle diameter. The smallest particles of 100 µm are referred to as flocs, while all larger particles are considered (proto-) granules.

Microbial ecology

The microbial population differs over the radius of the biofilm due to concentration gradients of substrates [Picioreanu et al., 1998]. Different organisms present in the biofilm are responsible for processes like nitrification, denitrification and phosphate removal [de Kreuk et al., 2005, Winkler et al., 2013]. However, since the aim of this study was to investigate the impact of the different mechanisms on the growth of aerobic granules, the biomass clusters are assumed to have constant ecology. Furthermore, biomass formation in wastewater treatment plants is mostly related to COD conversions. No nitrogen and phosphorus conversions are considered in the model as they contribute marginally to biomass formation. All modelled biomass can store COD anaerobically as storage polymers. Therefore, only the conversions of COD into storage polymers, and storage polymers into biomass, were simulated to describe granular growth.

Biological fate of COD-types in wastewater

The chemical oxygen demand (COD) present in domestic wastewater can be divided into multiple fractions [Henze, 1992]. These fractions can be divided based on the availability for biological conversions [Layer et al., 2019]. The soluble and suspended inert COD and inorganic solids are not available for any biological conversion and are thus disregarded in this model. Both the soluble readily biodegradable COD and the colloid fast hydrolysable COD are available for anaerobic conversion into storage polymers and are thus categorized as GFS. The suspended slowly hydrolysable COD is available for biological conversions, but not for anaerobic storage and are categorized as n-GFS. A schematic representation is shown in Fig. 44.

Model description

Fig. 44 Model overview, with (1) convection and dispersion in the bulk liquid, (2) mass transfer through the boundary layer, (3) 1D radial diffusion, (4) conversion of GFS to PHA, (5) settling of granules in the reactor, (6) individual based population model, (7) breakage. Schematic representation of the translation from organic substrates in ASM2d [Henze et al., 1999] into the granulation model (8).

Four mathematical models were combined to perform a sensitivity analysis on the hypothesized main mechanisms for aerobic granulation (see also Fig. 44). The four model components are described below.

• Cluster-based biomass population model: An AGS reactor typically contains a dynamic distribution of granule sizes, all of different age, shape and ecology. To capture the probability of granules of similar size to be at the different locations in the reactor at the same time, a cluster-based approach was used. The sludge population was discretized into clusters of aggregates with the same diameter, where each simulated cluster represented the same amount of physical biomass in the reactor. The amount of biomass represented by a cluster scaled linearly with the surface area of the simulated reactor, since the spatial gradients in an AGS reactor are mainly 1D (i.e. over the height). A convergence analysis showed that a discretization of 1.75 x 10^-2 simulated mass per real mass per reactor area (kg kg^-1 m^-2) yielded a discretization-independent solution. This resulted in 10,000 clusters at start-up in the reference case with only flocs of 100 µm, and the population increased to 100,000 upon successful granulation. New clusters were formed from n-GFS as clusters with a diameter of 100 µm. The clusters could be subjected to the following mechanisms:

  • Growth: in the reaction phase, the diameter of each cluster of particles grew according to the amount of PHA formed during the anaerobic feeding phase. This resulted in a different increase in volume for each cluster of granules. The increase was based on an apparent yield coefficient (including decay) and a constant biomass concentration in the granule, resulting in a constant VSS/TSS ratio. All PHA was assumed to be consumed and converted to new biomass, without any time dependence in the reaction phase.

  • Breakage: the larger aerobic granules become, the more likely they will break up into smaller pieces [de Graaff et al., 2020]. In the model, granule clusters larger than 3 mm have an increasing chance of breaking (increasing to 99 % for granules larger than 5 mm). Breakage leads to two clusters with random diameter between 100 µm and the original diameter, with a combined biomass equal to the original cluster.

  • Redistribution: if a cluster of granules exceeded the maximum amount of represented real biomass, it was split into two clusters of granules with same diameter. Each cluster would represent half of the original biomass.

  • Wasting: Biomass discharge from the reactor was performed by the removal of number of complete clusters. Clusters were selected, depending on the wasting method used (a mixed sample for MLSS control or based on settling velocity for selective wasting).

• Bulk-liquid solute mass balance: the anaerobic feeding in an AGS reactor is mainly a 1D process, since reactors are fed from the bottom and the process is designed to get an optimal plug flow. Some axial mixing does occur [van Dijk et al., 2018]. Therefore, the concentration profile of GFS during feeding was described by an 1D convection-dispersion model [Degaleesan and Dudukovic, 1998, van Dijk et al., 2018]. It was solved with one-way coupling to the settling model, since during the feeding phase granules will still be settling and partially fluidize. The calculated effective voidage is thus dynamic and will influence the local fluid velocity.

• Biofilm solute mass balance: The flux of GFS into a granule depends on the local concentration in the bulk-liquid surrounding the granule and the rate of mass transfer, which varies over the height of the reactor. It is in turn affected by the rate of diffusion in the granules and rate of reaction of GFS to PHA. Furthermore, anaerobic storage capacity of PHA is limited by a maximum PHA content, used as a simplification for depletion of glycogen [de Kreuk et al., 2007]. The dynamic mass balances of GFS and PHA were modelled using a 1D radial reaction-diffusion model for each cluster of particles, solved fully coupled to the bulk-liquid mass balance. The combined processes in the bulk-liquid phase, biofilm phase and the settling model determined the total amount of storage polymer per cluster of granules after the feeding phase.

• Settling model: the settling velocity of a granule depends on the physical properties of the granule (size and density) and the biomass concentration in the near vicinity of the granule. As a result, every granule will have a unique settling velocity, eventually determining the position in the reactor during feeding. To describe this settling behaviour, we used the Van Dijk settling model [van Dijk et al., 2020] and adapted it to describe the settling and fluidization of clusters of granules. The model was also adapted to better describe the settling of flocs and proto-granules. The latter involved a change in the calculation of the expansion index, which is now calculated based on the Archimedes number.

Mathematical model

The model consists of several components to simulate the change in time and in space of the dependent variables listed in Table 9.

Table 9 Dependent variables and interdependence in submodels. An ‘X’ denotes that the variable is used in a submodel. An ‘O’ indicates that the variable is dynamically computed in that submodel. Arrows indicate the extent of coupling between submodels (either one-way coupled (\(\leftarrow\) or \(\rightarrow\)) or fully coupled (\(\leftarrow\rightarrow\))). Subscript j denotes the index of the cluster of sludge particles.

	Bulk-liquid solute mass balance	Biofilm solute mass balance	Settling model	Granule population model
\(c_{GFS, L}(x, t)\)	O\(\rightarrow\)	\(\leftarrow\)X		X
\(c_{GFS, B, j}(r, t)\)	X\(\rightarrow\)	\(\leftarrow\)O\(\rightarrow\)		X
\(c_{PHA, B, j}(r, t)\)		O\(\rightarrow\)		X
\(x_{j}(t)\)	X	X	\(\leftarrow\)O
\(d_{j}(t)\)	X	X	X	\(\leftarrow\)O

Bulk-liquid solute mass balance

The mass balance of GFS during anaerobic feeding was formulated as follows, describing axial dispersion, convective transport and mass transfer between the bulk and the biofilm (from/to all granules in the set of clusters \({N_i}\) at a certain height):

(33)\[ \frac{{\partial {c_{GFS,L}}}}{{\partial t}} = - {D_{ax}}\frac{{{\partial ^2}{c_{GFS,L}}}}{{\partial {x^2}}} + \frac{{{v_{in}}}}{{{\epsilon _L}(x)}}\frac{{\partial {c_{GFS,L}}}}{{\partial x}} + \sum\limits_{j = 1}^{{N_i}} {{k_{LB,GFS}}} \frac{{{a_j}}}{{{\epsilon _L}(x)}}({c_{GFS,B,j}}{|_{r = {d_j}/2}} - {c_{GFS,L}})\]

For the bottom inlet boundary we used a Danckwerts condition:

\[ {\left. {\left( {\frac{{{v_{in}}}}{{{\epsilon _L}(x)}}{c_{GFS, L}} - {D_{ax}}\frac{{\partial {c_{GFS, L}}}}{{\partial x}}} \right)} \right|_{x = 0}} = {v_{in}}{c_{GFS, in}}, t > 0 \]

The top outlet boundary was based on a zero zero-dispersion condition:

\[ {\left. { - {D_{ax}}\frac{{\partial {c_{GFS,L}}}}{{\partial x}}} \right|_{x = H}} = 0,t > 0\]

Biofilm phase solute mass balance

The mass balance of GFS and storage polymers (PHA) over the biofilm phase was modelled according to the following equation:

\[ \begin{align}\begin{aligned} \begin{array}{l}\\\begin{split} \frac{{\partial {c_{GFS,B,j}}}}{{\partial t}} = \\\end{split}\\ - {D_{GFS,B}}\left( {\frac{{{\partial ^2}{c_{GFS,B,j}}}}{{\partial {r^2}}} + \frac{2}{r}\frac{{\partial {c_{GFS,B,j}}}}{{\partial r}}} \right) + {R_{GFS}}\left( {{c_{GFS,B,j}}(r),{c_{PHA,B,j}}(r)} \right) \end{array} \end{aligned}\end{align} \]

and

\[ \frac{{\partial {c_{PHA,B,j}}}}{{\partial t}} = {R_{PHA}}\left( {{c_{GFS,B,j}}(r),{c_{PHA,B,j}}(r)} \right)\]

Here the volumetric reaction rate R is based on Monod kinetics [de Kreuk et al., 2007] . Both Monod constants are two orders of magnitude smaller than the actual concentrations, therefore practically serve as switching terms:

\[ \begin{align}\begin{aligned} \begin{array}{l}\\\begin{split} {R_{GFS}} = {q_{AN,\max }}X\frac{{{c_{GFS,B,j}}}}{{{K_{GFS}} + {c_{GFS,B,j}}}}\frac{{{c_{PHA,\max }} - {c_{PHA,B,j}}}}{{{K_{PHA}} + {c_{PHA,\max }} - {c_{PHA,B,j}}}} \\ {R_{PHA}} = - {R_{GFS}}\end{split}\\ \end{array} \end{aligned}\end{align} \]

On the biofilm surface the boundary was defined through flux-continuity with transfer in both directions between bulk-liquid and biofilm:

\[ {\left. { - {D_{GFS,B}}\frac{{\partial {c_{GFS,B,j}}}}{{\partial r}}} \right|_{r = {d_j}/2}} = {k_{LB,GFS}}({c_{GFS,B,j}}{|_{r = {d_j}/2}} - {c_{GFS,L}}{|_{x = {x_j}}}),t > 0\]

The boundary in the centre of the biofilm was defined through symmetry:

\[ {\left. { - {D_{GFS, B}}\frac{{\partial {c_{GFS, B, j}}}}{{\partial r}}} \right|_{r = 0}} = 0, t > 0 \]

Mass transfer between bulk-liquid and biofilm

The mass transfer coefficient was calculated based on Sherwood relations for forced convection around a free sphere [Cussler, 2009] (top relation) or semi-fluidized beds [Fan et al., 1960] (bottom relation). The choice depended on the local voidage of the sludge bed during feeding since no relation covered the complete voidage range (from settled granular bed (0.5) to nearly void of biomass):

\[\begin{split} {k_{LB,GFS}}\left( {{\epsilon _L},{d_j}} \right) = \max \left( {\begin{array}{*{20}{c}} {\left( {2.0 + 0.6{{\left( {\frac{{{d_j}{v_{in}}}}{{\nu {\epsilon _L}}}} \right)}^{\frac{1}{2}}}{{\left( {\frac{\nu }{{{D_{GFS,L}}}}} \right)}^{\frac{1}{3}}}} \right)\frac{{{D_{GFS,L}}}}{{{d_j}}}} \\ {\left( {2.0 + 1.51{{\left( {(1 - {\epsilon _L})\frac{{{d_j}{v_{in}}}}{\nu }} \right)}^{\frac{1}{2}}}{{\left( {\frac{\nu }{{{D_{GFS,L}}}}} \right)}^{\frac{1}{3}}}} \right)\frac{{{D_{GFS,L}}}}{{{d_j}}}} \end{array}} \right)\end{split}\]

Settling model

The settling model from chapter Settling behaviour was used to describe the settling of the individual groups of granules. Since this model only describes the settling behaviour of classes of granules, it was adapted to describe the settling behaviour of individual clusters of granules of the same size (j):

(34)\[ {v_j} = k{v_{f, j}}{\epsilon _j}^{{n_j} - 2}\frac{{{\rho _{B, j}} - {\rho _{bed, i}}}}{{{\rho _{B, j}} - {\rho _L}}}.\]

Furthermore, every cluster of granules (instead of classes) experienced an apparent voidage fraction of the surrounding liquid \(\epsilon_L\). The calculation of this apparent voidage fraction for individual granules is identical to the calculation for granule classes, only in this case is the diameter represents the individual granule instead of the granule class.

\[ {\epsilon _j} = \;1 - \;{\left[ {1 + \left( {\frac{{{\overline{d_i}}}}{{{d_j}}}} \right)\left[ {{{\left( {1 - {\epsilon _L}} \right)}^{ - \frac{1}{3}}} - 1} \right]} \right]^{ - 3}}\]

Similarly, the average granule diameter can be calculated based on groups of similarly sized granules at the same height in the reactor:

\[ {\overline{d_{i}}} = \frac{{\sum\limits_{j = 1}^{{N_i}} {{\theta_j}{d_j}} }}{{1 - {\epsilon _L}}} \]

Although this approach works well for classes of granules, the model outcome is unrealistic when a large granule is surrounded by lots of small granules or flocs. Here \(\overline{d_{i}}\) will approach the size of the flocs in this case, leading to a very low value of \(\epsilon_j\) for the large granule. The resulting low value of \({{\overline {{d_i}} } \over {{d_j}}}\) makes the large granules stop settling all together. To cope with these rare cases, the value of \(\epsilon_j\) is set to \(\epsilon_L\) when \(\epsilon_j-\epsilon_L < 0.1\).

In chapter Settling behaviour the ratio between the fluidizing velocity and the terminal velocity was found to be 0.5, after calibration with a single fraction between 1.0 and 2.0 mm. In this study we found that a value of 0.8 would give a better estimate for the smallest size fraction between 100 and 200 µm, and still agree with the original data. A similar correction was made for the calculation of the expansion index. In this case it was calculated based on the Archimedes number [Andalib et al., 2012]:

(35)\[ n_j= \frac{1}{9.143 \cdot 10^{-6} Ar^{0.7728} + 0.2}\]

The position of a cluster of granules during feeding or settling (i.e. \(v_{in} = 0\)) was modelled as follows:

\[ {{d{x_j}} \over {dt}} = {v_j} + {v_{in}} \]

Growth of granules within a cluster

During each reaction phase, the volume (and thus the diameter) of a granule cluster was increased according to the amount of GFS accumulated as storage polymers during the anaerobic feeding phase, and a constant density and apparent yield throughout the granule. The new diameter of a granule cluster (j) was calculated using the following equation, assuming a spherical geometry:

\[ {d_j} = 2{\left( {{{{V_{j,old}} + {{{Y_{X,PHA}}} \over {{c_X}}}\int_0^{{d_{j,old}}/2} {{c_{PHA,j}}} A{\mkern 1mu} dr} \over {{4 \over 3}\pi}}} \right)^{{1 \over 3}}}\]

Breakage of biofilm clusters

The probability of breakage is calculated with a logistic function:

\[ P_j = \frac{1}{e^{-5000*(d_j-0.004)}+1} \]

Aerobic reaction phase

Processes taking place during the reaction phase were not modelled with time dependence, nor with a spatial dependence, but as a sequence of events. First, the residual GFS that was not stored anaerobically was distributed over all existing clusters based on specific biofilm surface area. Next, the diameter of all clusters was increased due to growth, based on an apparent yield (i.e. including loss from decay). All n-GFS fed during the anaerobic phase was subsequently converted into new flocs. The final step was breakage of particles. This is different from the time dependent approach often used in single biofilm modelling [Wanner and Reichert, 1996], but the simplification was justified due to the requirement of a discrete, cluster-based approach. Mixed wasting of sludge was applied for MLSS control at the end of the aeration phase.

Cycle build-up

A typical Nereda^® cycle was simulated in the model. This typical cycle has a duration of 6 hours, and consists of 60 min of anaerobic feeding and decanting, 270 min of reaction time, and 30 min for settling and wasting of biomass. These typical values could vary in the scenarios. Fig. 45 shows the different processes being modelled in the different phases of the cycle.

Fig. 45 Typical batch scheduling for the AGS process and the various active processes in the model.

Table 10 Biological and physical constants used for the sensitivity analyses.

Constant	Symbol	Value	Unit	Reference
Péclet number	\(Pe\)	2.5 x 102	-	[van Dijk et al., 2018]
Reactor height	\(H\)	6	m	this study
Feeding velocity	\({v_{in}}\)	4	m h-1	this study
Bulk-liquid density	\(\rho_{{L}}\)	1 x 103	kg m-3	[van Dijk et al., 2020]
Granule density	\(\rho_{{B}}\)	1.035 x 103	kg m-3	[van Dijk et al., 2020]
Temperature	\(T\)	293	K	this study
Biomass concentration granule	\({c_X}\)	5 x 101	kg m-3	[van Dijk et al., 2020]
Diffusion coefficient GFS in bulk (298 K)	\({D_{GFS,L}}\)	1.21 x 10-9	m2 s-1	[Cussler, 2009]
Diffusion coefficient GFS in biofilm (298 K)	\({D_{GFS,B}}\)	2.4 x 10-10	m2 s-1	[van den Berg et al., 2021]
Monod constant for GFS	\({{K_{GFS}}}\)	1 x 10-3	kg m-3	this study
Monod constant for PHA	\({{K_{PHA}}}\)	1 x 10-3	kg m-3	this study
Maximum biomass specific substrate uptake rate	\({q_{AN,max}}\)	2.78 x 10-5	kg kg-1 s-1	this study
Maximum storage capacity of GFS	\({{c_{PHA,max}}}\)	7.5	kg m-3	this study
Yield of biomass on storage polymers	\({Y_{X,PHA}}\)	0.32	kg kg-1	this study
Yield of biomass on n-GFS	\({Y_{X,n\text -GFS}}\)	0.32	kg kg-1	this study

Lorenz-curve and Gini-coefficient

For analyses of the model result, we used a method for calculating inequality called the Gini coefficient [Gini, 1912]. This Gini coefficient quantifies the inequality using the Lorenz-curve, which plots the cumulative fraction of the total income (y-axis) earned by a population fraction sorted (x-axis) [Lorenz, 1905]. The Gini coefficient is determined by the ratio of the area between the equality line and the Lorenz curve, and the area below the Lorenz curve. To utilize the Gini coefficient for the quantitative analysis of the distribution of GFS in the feeding phase, the amount of GFS accumulated as storage polymers by each cluster was calculated weighted by the number of granules (G) represented by a simulated cluster (j). Before calculation, the clusters were sorted based on the amount of accumulated GFS from low to high. The y-axis of the Lorenz curve was defined as:

\[ {y_j} = {{\sum\limits_{m = 1}^j {{G_m}\int_0^{{d_m}/2} {{c_{PHA,m}}A{\mkern 1mu} dr} } } \over {\sum\limits_{m = 1}^N {{G_m}} \int_0^{{d_m}/2} {{c_{PHA,m}}A{\mkern 1mu} dr} }} \]

The x-axis was calculated via:

\[ {x_j} = {{\sum\limits_{m = 1}^j {{G_m}} } \over {\sum\limits_{m = 1}^N {{G_m}} }}\]

Size distribution

The granule size distribution of the sludge in the Nereda^® reactor used as reference in Fig. 42 was measured over time. To determine the granule size distribution 1 L of sample was poured over a series of sieves with different mesh sizes ( 212, 425, 630, 1000, 1400, and 2000 µm). A mixed sample of 100 mL was filtered for the determination of the total dry weight. The obtained granular biomass of the different sieve fractions and the mixed sample were dried at 105 °C until no change in weight was detected anymore. Then the sieve fractions are grouped together: small granules are the sum of 212, 425 and 630 µm, large granules are the sum of 1000, 1400 and 2000 µm and the concentration of proto-granules and flocs is obtained by subtracting the sum of all granule fractions from the concentration of the mixed sample.

Results and discussion

A sensitivity analysis was done to compare the influence of the major mechanisms on the granulation process. The main results for all scenarios are summarized in Table 11 and Fig. 46.

Fig. 46 Concentration and evolution of granule fractions in the scenarios: blue area shows flocs and proto-granules, green area shows small granules, orange area shows large granules. R: reference case, A: mixed feeding, B: 15 min feeding, C: 30 min feeding, D: no selective wasting, E: 100 mg L^-1 GFS, F: no selective feeding.

Reference case

A reference case was defined and the different scenarios in the sensitivity analysis were compared to this reference case. The reference case was a full-scale reactor with a water depth of 6 m, that was seeded with 2 g L^-1 of flocs of 200 µm. The selection pressure at the start was 3 m h^-1 and it was slowly increased whenever the sludge concentration reached 3.0 g L^-1. The reactor was fed from the bottom of the reactor, with a P’eclet number of 250. The exchange ratio was 25 % and there were no rainy weather conditions, or other variation to the influent flow or composition. The reactor was fed four batches per day, containing 500 mg L^-1 of COD, which was composed of 200 mg L^-1 granule forming substrate and 300 mg L^-1 non-granule forming substrate. The feeding time was 60 min. Feeding and decanting was done simultaneously, as is normal for full-scale AGS installations.

For analyses the particles in the reactor are classified in three main types: the proto granules, which are particles in the range of 100 - 200 µm. These particles have the granular morphology, but settling behaviour is floc-like, so they are not able to separate from the sludge matrix. Flocs are mathematically treated similar to the proto-granules, because they both have the same floc-like behaviour. In the model a floc is represented by particles of 200 µm and smaller. Small granules are particles in the range of 200 - 1000 µm. These particles (larger than 200 µm) are aerobic granules according to the definition of AGS [de Kreuk et al., 2007]. These granules settle better than the proto-granule fraction and are small enough to be fully penetrated with substrate (acetate and oxygen). Particles larger than 200 µm are called large granules. These granules settle very quickly and accumulate near the bottom of the reactor during the feeding phase. Large granules are large enough to only be partially penetrated with substrates.

The granulation process in the reference case is shown in Fig. 46. Since the reactor is seeded with particles of 200 µm, it takes time before the first small granules appear in the reactor. All proto-granules have the same bulk-like settling behaviour, so selective wasting has no effect yet. This means every particle has the same chance of being spilled. Until this point the growth of the granules is based on chance. The proto-granules will not not receive substrate every cycle. The substrate load depends on the position in the sludge bed, the volumetric exchange ratio and the amount of sequestered substrate by the particles beneath it. Over the course of multiple cycles, the combination of these factors will determine whether a proto-granule will receive enough substrate to grow into a small granule before it is spilled.

After 90 d the first small granules appear, and these granules settle faster than the proto-granules. This gives these granules a competitive advantage: the granules will be fed more frequently, because they settle towards the bottom of the reactor. This can be seen as a race towards the substrate. The fastest settling granule will always win the race and can take up a maximum amount of substrate. On top of this, the fastest settling granule will also be spilled less likely in the selective wasting from the top of the settled sludge bed. Larger granules therefore have a double benefit: they receive more substrate and they are less likely to be spilled. This process is also visible in Fig. 46: small granules dominate the population in the reactor a few weeks after the first small granules appeared.

In the simulation the first large granules appear after 165 d. These granules have better settling properties then the small granules, the largest ones having settling velocities well over 100 m h^-1. This means the large granules will reach the bottom of the reactor in several minutes and they will be fed every cycle. The chance of being spilled through selective wasting is close to zero, because the settling velocity of large granules is much larger than the maximum applied selection pressure of 6 m h^-1. This is a matter of the winner takes it all. The large granules will accumulate most of the granule forming substrate (Fig. 47), essentially leading to the extinction of the proto-granules.

The end of the lag phase is defined as the moment the biomass concentration increases more than 10 % above the target concentration of 3 g L^-1. This means the maximum selection pressure of 6 m h^-1 is reached and due to the increasing amount of granules, the biomass concentrations keeps increasing. The reference case has a lag phase of 193 d. The end of the lag phase marks the start of the granulation phase, which ends when the target biomass concentration of 8 g L^-1 is reached. Hereafter the biomass concentration is kept on 8 g L^-1 through mixed wasting in the aeration phase. The duration of the granulation phase was 58 d (see Table 11).

The granulation process in the reference case is very similar to what is observed in practice (Fig. 42). It shows a similar apparent steady state in the lag phase after which large granules appear in the granulation phase. Granulation in practice shows a bit more variation due to processes that are not taken into account in the model, such as rain weather events, load variations and temperature variations, but the overall process compares well.

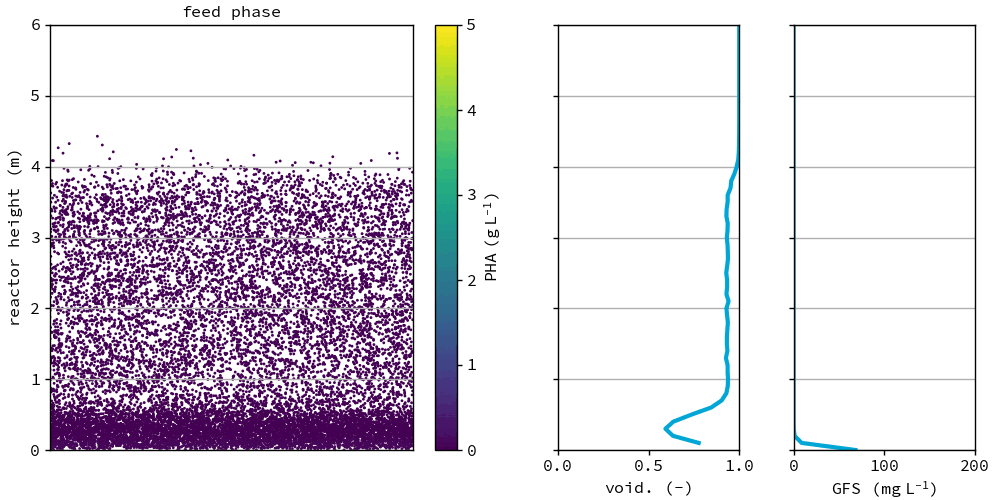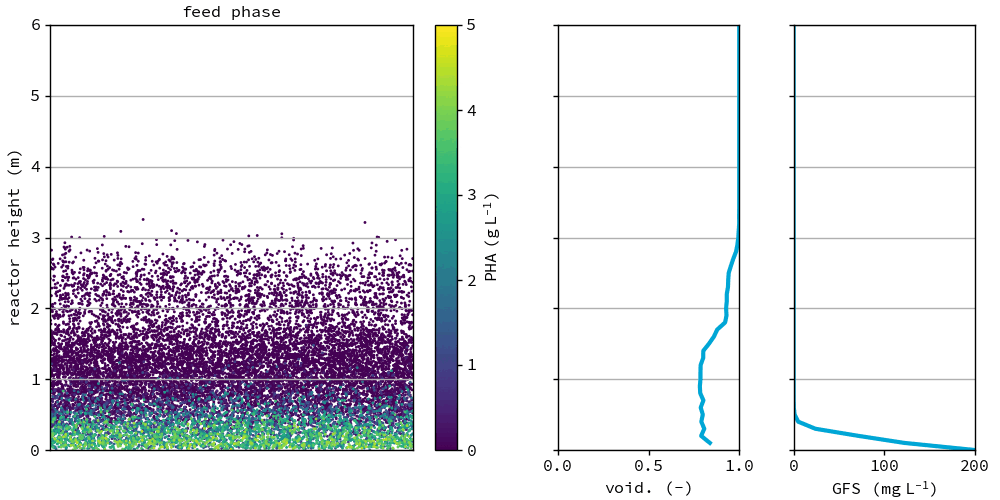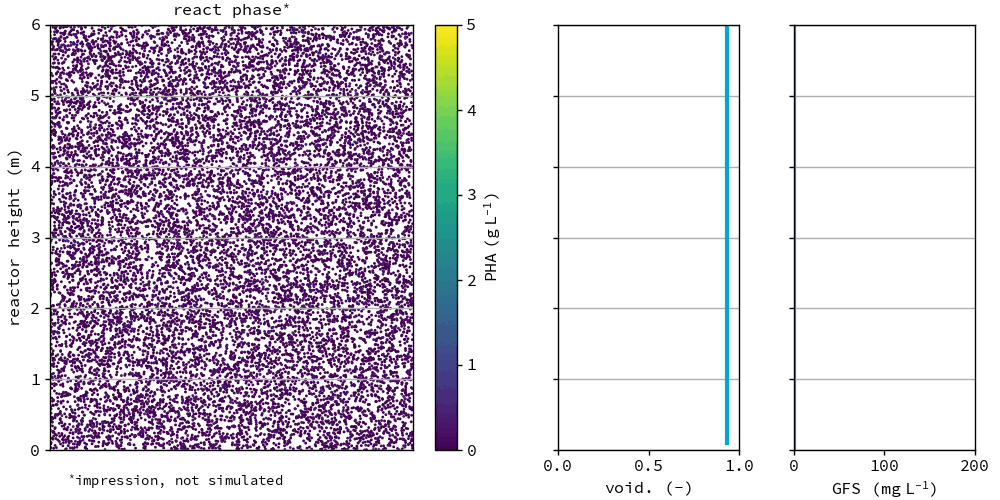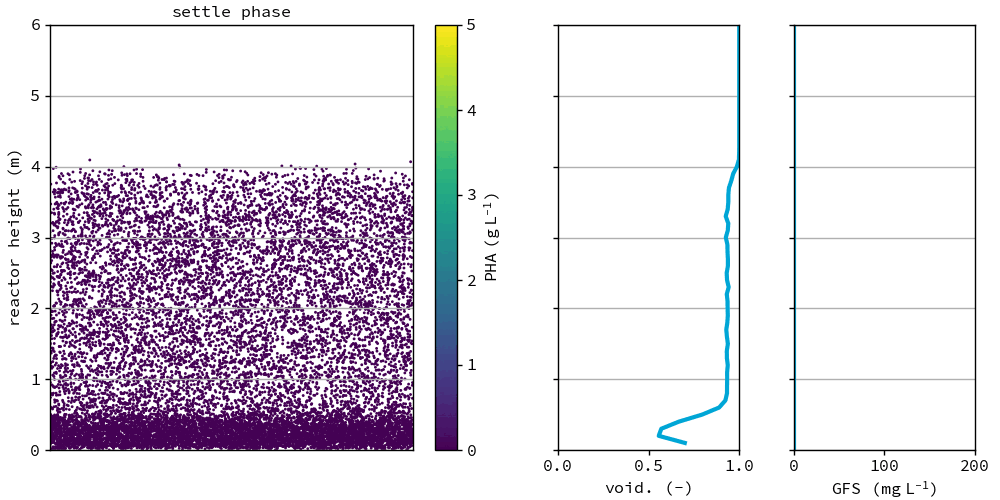
Fig. 47 Granules in the reference after the feeding phase at day 75. All graphs show the depth of the reactor on the y-axis. Left: individual groups of granules, color based on PHA concentration in the granule, x location is randomly chosen for visualization. Middle: the voidage fraction in the bed. Right: granule forming substrate in the bulk liquid.

Table 11 Results of sensitivity analysis.

	first granule		phases		granule size
	small	large	lag	granulation	average	maximum
	(d)	(d)	(d)	(d)	(200 µm)	(200 µm)
reference case	90	165	193	58	1371	3742
no plug flow	78	-	205	73	695	742
15 minutes feeding	125	278	290	42	1206	2399
30 minutes feeding	95	203	205	42	1575	3716
no selective wasting	98	193	-	-	189	3518
100 mg L-1 GFS	-	-	-	-	110	736
no selective feeding	115	278	275	52	1126	3886

Microbial selection

The effect of changing feast/famine conditions was shown by shortening the anaerobic feeding time, thus limiting the anaerobic uptake of granule forming substrate. Since the batch size (and thus the loading rate) was kept constant, shortening the feeding time resulted in a higher feed flow velocity. In the reference case the anaerobic feeding time was 60 min, which was reduced to 30 min and 15 min. The shorter feeding time has a clear effect on the duration of the lag phase, which was 193 d in the reference case and was increased to 290 d in the case with a 15 min feeding phase (table {\ref{tab:sensitivity_analysis}). The granulation phase was a bit faster, when the feeding phase was shortened, reducing from 58 to 42 d. The final granule size distribution after 365 d was quite similar.

The difference in the lag phase is a consequence of the higher up-flow velocity and the shorter contact time in the scenarios. A consequence of the higher up-flow velocity is a larger sludge bed expansion, leading to less proto-granules in contact with the influent. The shorter contact time also leads to less uptake of substrate by the particles. As a result, less proto-granules grow into small granules due to the more even distribution of the residual granule forming substrate left over after the feeding phase.

In the granulation phase the bed expansion is no issue anymore, because small granules can settle faster than flocs and proto-granules. So, the substrate-rich influent is more effectively in contact with the largest granule size fraction. The higher up-flow velocity causes a distribution of the GFS to be more skewed towards the small granules. As a result, small granules are converted into larger granules more quickly, slightly reducing length of the granulation phase.

Overall, the duration of the feast period is especially important in the lag phase, which is shortened by a longer feast period at equal daily volumetric loading rates. In the granulation period, the duration of the feast period is of less importance and might even provide a means to control the granule size distribution.

Selective wasting

The contribution of selective wasting to the aerobic granulation process was shown by switching from selective wasting to mixed wasting. In selective wasting the slowest settling biomass is removed from the top of the sludge bed, while faster settling particles remain in the reactor. In mixed wasting, the biomass concentration is kept constant by wasting both fast and slow settling biomass, all particles having the same chance to be spilled. The mixed wasting is representative for the situation in a conventional activated sludge process. The biomass was spilled to maintain a concentration of 3 g L^-1. This mixed wasting did not lead to a significant granular fraction, although after 98 d the first small granules appeared in the reactor. Some large granules were present at the end of the simulation, although their contribution was small (0.3 g L^-1) and with insufficient effect on the settleablility to allow for an increase in MLSS.

This scenario clearly shows the importance of selective wasting, because without it, significant granulation does not happen. It also shows the drive towards granulation from the other mechanisms in the reactor. Although the granules are not preferentially maintained in the reactor as they are randomly spilled, new granules are constantly formed, due to spread in anaerobic distribution of GFS. This might explain, why (small) granules are observed in many conventional activated sludge systems [Wei et al., 2020] . Even without selective wasting, some growth of granules can happen, when the other drivers for granulation are sufficiently present in the reactor. However, selective wasting is essential to drive the sludge towards full granulation.

Concentration gradients

To show the positive effect of upwards plug flow feeding on the granule formation, in the simulation the plug flow feeding was removed. The reactor was changed into an ideally mixed reactor during the feeding period. In full-scale AGS reactor feeding and decanting is done simultaneously, which is possible because of the plug flow [van Dijk et al., 2018] . When the reactor would be ideally mixed during feeding, biomass would wash-out, resulting in poor effluent quality. For a good comparison between the scenarios, in the simulation biomass was not allowed to leave the reactor with the effluent. The results show a strong shift towards smaller granules. Compared to the reference case the duration of the lag phase was only slightly longer (205 d compared to 193 d). Also, the duration of granulation phase was very similar. The real difference is visible in the granule size distribution at the end of the simulation. Without the plug flow feeding, no large granules appeared in the reactor and the average granule size was 200 µm (compared to 200 µm in the reference case).

This shift towards smaller granules is caused by several different processes. Lower substrate concentrations in the bulk liquid limit the diffusion depth of substrate into the granules. This results in slower granule growth. Also, all substrate is distributed evenly over all particles, where in the reference case the best settling fraction receives most of the substrate. Pilot-scale work with anaerobic pulse-feeding of municipal wastewater showed a smaller mean granule size compared to the plug flow of full-scale bottom-fed reactors [Rocktäschel et al., 2015] . Because the other mechanisms for granulation are still present (microbial selection, selective wasting and granule forming substrate), the system can still achieve a high granulation grade, but only with small granules.

Selective feeding

The effect of the selective feeding was shown by removing the differences in settling velocity between the different particle sizes during the feeding phase. As a result, all particles have the same chance to be exposed to substrate, regardless of their settling properties, while the concentration gradient resulting from the plug flow was kept intact. The effect is most noticeable in the duration of the lag phase, which takes 275 d compared to 193 d in the reference case. The duration of granulation phase is comparable with the reference case, but the granulation phase starts without any large granules present. In the end the average granule size is slightly smaller than in the reference case. This outcome indicates that whether a system transitions from the lag phase to the granulation phase is not only determined by the formation of some small granules that settle faster than proto-granules and flocs. The ability to exploit the faster settling properties of small granules for the uptake of GFS is key in accelerating the transition from the lag-phase to the granulation-phase and of the granulation phase itself.

The selective feeding can thus be seen as a race to the substrate: the best settling granules will have the longest exposure to the substrate and will see the highest concentration gradients. Because the settling properties of granules get better as they get larger, selective feeding allows for an increase substrate utilization with an increasing granule size. Removing selective feeding from the simulation shows, as expected, a shift towards smaller granules. Although in the end large granules still appear in the reactor, selective feeding is an important driver for granulation, which has not been recognized before in literature.

Granule forming substrate

In the model non-granule forming substrate will always lead to the formation of flocs and granule forming substrate can lead to the formation of granules, if it is converted into storage polymers. Especially in the lag phase the ratio between GFS and n-GFS will influence the chance of proto-granules to grow into small granules. When too many flocs are formed compared to the growth of the proto-granules, the proto-granules will get spilled before they grow into small granules and can preferentially be retained in the reactor. This is clearly shown in the scenario where the GFS was reduced from 200 mg L^-1 to 100 mg L^-1 (i.e. decreased from 40 % to 20 % of the influent COD). Under these conditions the lag phase does not finish in the 365 d of simulation. Although some small granules appear in the reactor (the maximum granule size is 200 µm), the average granule size is only 200 µm and the simulation clearly shows a shift towards flocs in the lag phase.

In the model transport and conversion characteristics of GFS were modelled as acetate, which is the most abundant granule forming substrate in municipal wastewater treatment. GFS is derived from the fatty acids in the influent supplemented with the fatty acids formed by fermentation and hydrolysis of more complex influent COD [Layer et al., 2019, Toja Ortega et al., 2021] . The amount of GFS is in this context partly depending on the process conditions. Fermentation and hydrolysis were not included in the presented modelling framework, since for this sensitivity analysis the origin of the GFS is not important. The amount of GFS will determine if the wastewater is suitable for AGS. For future modelling and better design of AGS processes these fermentation and hydrolysis processes will need better characterization in order to include them in a reliable manner in aerobic granular sludge simulation platforms.

Breakage

Granules will eventually break into smaller pieces. In the model the chance of breaking is coupled to the granule size: larger granules have higher chance of breaking. The resulting pieces can become a seed for new granules. In the simulations the origin of granules (floc or breakage) was monitored. At the start, all granules originate from flocs. When large granules appear in the reactor, an increasing fraction of the biomass originates from broken-up granules. At the end of the simulation (after 365 d) almost 20 % originates from broken-up large granules. This process can be seen as a bypass of the lag phase. Some pieces will be larger than proto-granules and can develop into new granules, without going through the stochastic growth process of the proto-granules. In this work, the probability of breakage was increased with increasing granule size, based on a decreasing granule strength, as was reported by [de Graaff et al., 2020] . The granule size beyond which a granule would have a definite probability to break-up was based on the maximum granule size observed in full scale Nereda^® [van Dijk et al., 2020] . Granules can break-up in two parts of random volume, adding up to the volume of the original granule. In practice, breakage into multiple parts as well as attrition will occur [Beeftink and van den Heuvel, 1990] . Reality is clearly more complicated than the implementation used for the sensitivity analysis in this study. However, all implementations would have the same qualitative effect as was observed in this study, determining the maximum granule size and generate nuclei of varying size for granulation to continue. For a part the breakage of large granules will be a driver for the acceleration of the granulation process in the granulation phase. Breakage of granules has a similar effect as adding an external seed of granules to a reactor [Pijuan et al., 2011] . Both act as a source of new granules, bypassing the slow stochastic process of growing small granules out of flocs and proto-granules. So during start-up of AGS systems in practice a granular seed could speed up start-up times significantly.

Model validity

Various mathematical models have been developed to describe biofilm growth [Wanner and Reichert, 1996] and biochemical conversions in (partially) aerobic reactors for wastewater treatment [Henze et al., 1999] . For the sensitivity analysis presented here, we opted to implement only conversions required to capture the basic dynamics a mechanism has on distribution of biomass over the size classes of granules. The model was intended for systems with an anaerobic feast phase and an aerobic famine phase. Only heterotrophic growth was assumed, with a constant VSS/TSS ratio, using two substrates (n-GFS and GFS) and an apparent yield for growth (modelling decay and growth combined). Consequently, the active biomass density was constant, homogeneous over the radius of a granule and independent of the historical substrate loading rate of a cluster. This history could also not impact the storage capacity of PHA. Regardless of these simplifications, the model was able to describe the principal behaviour of the granulation process, consisting of a lag phase and a granulation phase, without focus on mimicking actual reactor performance. In the future the model could be extended to incorporate biological nutrient removal to investigate the effects of the mechanisms on reactor performance.

Further analysis

The sensitivity analysis performed in this study shows how delicate the start-up of a AGS reactor from flocs is. The lag phase that is seen in practice can be explained by the slow stochastic process of turning flocs into proto-granules and proto-granules into small granules. Selective wasting is an important mechanism for granulation, but in the lag phase, because of the entrapment of proto-granules in the sludge flocs, it has a limited effect. Granules are only selectively retained in the reactor, when they settle faster than the flocculent sludge fraction. So the selective wasting only starts to be effective when small granules appear in the reactor. The lag phase seems to be mainly driven by the presence of granule forming substrate and the ratio between proto-granule growth and production of new flocs. The latter is important for the retention time distribution of the proto-granules. Flocs and proto-granules will have a different age. The distribution of age needs to allow for small granules to be formed, so the maximum retention time distribution determines, if and how fast small granules are formed.

In the granulation phase the other mechanisms become more important for the granulation process. Large granules will not be spilled through the selective wasting and will only disappear from the reactor through breakage. The largest granules receive the largest amount of substrate, because of the selective feeding. Their substrate uptake capacity combined with their abundance is large enough to take up all the substrate. As a consequence, only a limited amount of granule forming substrate is available for the flocs and proto-granules in a mature granular bed. The large granules will filter out all substrate from the influent at the bottom of the reactor. It is a matter of “the winner takes it all”, as can be seen in Fig. 48, where we used a Lorenz curve to visualize this process. In economics the Lorenz curve [Lorenz, 1905] is used to visualize the inequality of the wealth distribution. We used it to visualize the inequality in the substrate sequestered by the granules. The accompanying Gini coefficients [Gini, 1912] are also shown. In the plot the cumulative amount of substrate taken up by the granules was plotted versus the cumulative amount of granules. The diagonal line would represent a completely even distribution of the substrate over all granules. The Lorenz curve at 3 different days is plotted. At the start of the simulation there is some inequality, but this is caused by the batch size that is smaller than the bed height. At the end of the lag phase there is already a large inequality with a Gini coefficient increasing from 0.354 to 0.952, indicating a large change in substrate distribution. So at the end of the lag phase, already a large part of the substrate is sequestered by a small part of the granules. At the end of the granulation phase the inequality is even larger, with a Gini coefficient of 0.998, indicating that only a small fraction of granules sequester almost all the substrate, clearly showing the effect of the selective feeding.

Fig. 48 Lorenz curve showing the inequality in substrate distribution over the granules in the reference case. The curves are given at the start of the simulation, at the end of the lag phase and the end of the granulation phase, indicating an increasing inequality in substrate distribution. The numbers in the legend indicate the Gini coefficient (0 for equal distribution, 1 of complete unequal distribution).

Practical implications

Growing granules from activated sludge flocs in a full-scale reactor can be a lengthy process, as shown in Fig. 42. The model shows that a lag phase is a natural part of the granulation process. In practice reactors are often seeded with AGS from other plants to shorten the lag phase. Seeding is a method to break out of the stochastic processes that dominate the length of the lag-phase. Besides providing insights on the granulation process, the model can help to optimize the start-up process and find an optimum between cost for seeding and length of the start-up process. The model can also be used to optimize the start-up strategy regarding selective wasting, applied batch size and cycle times. When in the future the model is extended with a more elaborate biological model, it can also be used to investigate the effect of granule size distribution on conversion rates and effluent quality.

Conclusion

A model was developed to provide a theoretical framework to analyse the different relevant mechanisms for aerobic granular sludge formation, which can form the basis for a comprehensive model that includes detailed nutrient removal aspects. The insights from this study can be used to further improve the granule formation in AGS reactors.

• The model describes the dynamics of a lag and a granulation phase, found in practice.

• Selective feeding and breakage of large granules were identified as important mechanisms, not reported in literature.

• Granulation is a combined result from 6 mechanisms, allowing a sub-optimal mechanism to be compensated by the other mechanisms.

• The GFS/n-GFS ratio and feast/famine ratio are the most important mechanisms in determining whether a system can transition from the lag phase to the granulation phase.

• Selective wasting and selective feeding mainly determine whether the transition from lag to the granulation phase will occur and at which rate.

• Breaking of granules can have a positive effect on granulation, similar to seeding of reactors with granules.